
地坪缝的荷载传递
需要进行荷载传递的地坪实际自由边缘或角部相对少见,因为这些部位一般都只出现在建筑物的周线处。地坪板块之间的地坪缝及其交叉点则非常重要,因此在这些部位须设置荷载传递机制以免造成地坪板不均匀的竖向位移。通过地坪缝传递 50%以上的荷载是不可能的涂料在线coatingol.com。
对于下列地坪缝种类,其荷载传递须分别考量。
自由伸缩模板缝:地坪缝装置含有圆形或方形截面的传力杆或单独的传力板。
自由伸缩钢切健:将传力杆置于套筒内。锯切会诱导裂缝竖向贯穿整个地坪板,荷载传递由骨料咬合和传力杆提供。
限制伸缩模板缝:用设置传力钢筋的方法来限制接缝的自由伸缩,这些钢筋的布置方法与传力杆的布置方式相同,但在接缝两侧钢筋都须达到其锚固长度。钢筋的数量应与地坪板中钢筋数量对应,配筋率一般在0.08-0.125%的范围内。通常传力钢筋的直径为12mm,以间距450-600mm布置。
限制仲缩锯切缝(仅用于网片增强混凝土地坪板):锯切会诱导裂链竖向贯穿整个地坪板。但网片在切缝处连续,荷载传递由骨料咬合和网片提供。
1 、骨料咬合的荷载传递作用
骨料咬合是指狭窄不规则裂缝通过裂缝形成时两边暴露出来的骨料颗粒的相互接触,将荷载从一侧传递到另一侧的能力。其效果取决于锯切缝的张开宽度、地坪板厚、地基支承能力、荷载及其作用方式、以及骨料的棱角特性。显然,骨料只能在限制伸缩锯切缝处的诱导裂缝中或狭窄的随机裂缝中产生。
根据 Colley 和 Humphrey[54] 的研究,在设计应用中,张开宽度 1.5mm 的裂缝可以通过其传递15% 的荷载。在交通频繁或承受重型荷载的区域,当锯切缝或裂缝的张开宽度超过0.9mm 时,就应当对其进行充填,以恢复其骨料咬合能力。
因此设计方法为:

2、传力件或钢筋的荷载传递
传力件与钢筋的抗弯、抗剪承载力和劈裂力的计算方法可参看第6.5章节。对于土承地坪,承担荷载传递功能的传力件有效数量取外施荷载中心线两侧18 l距离范围内的传力件数量,其中l为相对刚度半径(Yoder and Witczak[55])。假定每个传力件承受的荷载随其与外施荷载中心线距离的增加而呈线性减小。这相当于假定中心线两侧0.9 l距离范围内的所有传力件都以其最大承载力工作。
受冲切承载力与地基支承
1、地坪板的受剪承载力
由于工业首层地坪的主要设计荷载是货架与叉车产生的点荷载,因此需要考虑其冲切作用。
受冲切承载力按照第6.4章节的方法通过验算荷载作用面积周线处的剪应力及距离荷载作用面积周边2.0d处临界截面周线处的剪应力来确定,这里的是指混凝土地坪板的截面有效高度。参看图7.8.
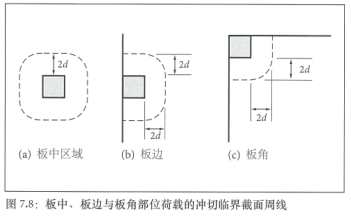
2、地基支承
由于假定地坪与垫层保持接触,冲切临界截面周线范围内的这部分荷载可以视作直接作用在地基上,因此设计作用力减小了。计算地基反力的方法如下:

然后,可以从作用力中扣除反力。
线载荷
这里采用了以Hetenyi [49]的研究为基础的弹性分析法。这种分析方法采用传统的综合安全系数1.5。由于已对材料性能采用了1.5的系数,不应再对荷载采用其它系数。用以确定土承地坪弯矩的等式采用了术语λ,其中:

由于该等式是以弯矩的弹性分布为基础的,Mun应当采用开裂弯距,也就是等式2中得到的数值。不应采用纤维增强混凝土板或网片增强混疑土板的残余弯矩(等式4的计算结果)。
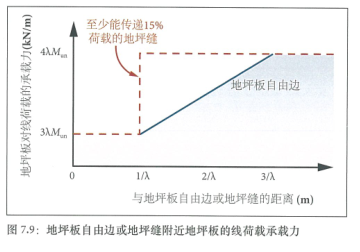
等式34适用于远离地坪缝或地坪板边的线荷载。地坪板在自由边处对线荷载的承载力为3λMun,并在距离自由边3/λ处增加到4λMun。如果地坪缝至少能够传递15%的荷载,则在距离地坪缝1/λ处的地坪板对线荷载的承载力可增加到4λMun一参看图7.9。
这种情况可以通过事实来说明:即对于远离地坪板边的线荷载,零弯矩的位置与荷载的距离大约为1/λ这与具有抗剪承载力但没有转动刚度的地坪缝情况相似。
均布荷载
这里采用了以Hetenyi[49]的研究为基础的弹性分析法。这种分析方法采用传统的综合安全系数1.5。由于已对材料性能采用了1.5的系数,不应再对荷载采用其它系数。和上述计算线荷载的情况一样,此处用以确定土承地坪弯矩的等式也采用了术语λ(等式33)。
下面的等式没有考虑均布荷载靠近地坪缝的情形。Hetenyi[49]对靠近地坪缝的均布荷载提供23了分析方法,但极其复杂。习惯上,计算均布荷载时都忽略地坪缝的因素,且已知这样不会导致地坪破坏。建议继续使用此方法,尽管设计师仍可参照Hetenyi[49]的方法更精确地对地坪板进行分析。
均布荷载的常见案例是堆载。一般情况下,地坪板会承受随机模型的均布荷载,但已经发现地坪板的最大正(下凸)弯矩是由作用宽度为π/2λ)的均布荷载引起的,如图7.10(a)所示。
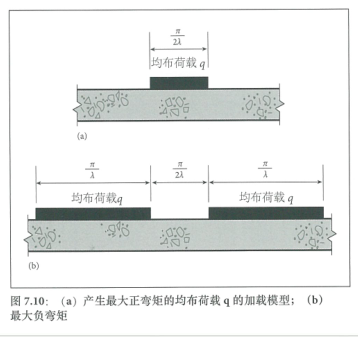
最大负(上凸)弯矩在一对均布荷载之间的位置产生,且每个均布荷载的作用宽度是π/λ,均布荷载间距为π/2λ,如图7.10(b)中所示。这个间距就是平时常说的临界巷道宽度。
单位面积的承载力,q,有下式得出:

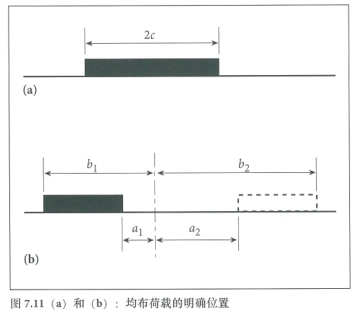
如均布荷载的作用位置已明确,Hetenyi[49]给出了由作用宽度为2c的均布荷载引起的正弯矩(如图7.22(a)中所示)的等式为:

在与均布荷载作用面的近端距离ɑ1处,即与均布荷载作用面远端距离b1处,参看图7.11(b),产生的负弯矩,Mn1,由下式得出:
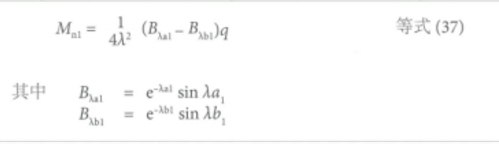
如果第二个均布荷载位置靠近第一个均布荷载,就会产生一个附加的弯矩Mn2,也由等式37确定,但需采用相应的ɑ和b值。因此q可以由(Mn1+Mn2)的最大值确定,将这个最大值等于混凝土板的负弯矩承载力Mn。
 涂料行业唯一!三棵树AI公益项目获艾菲国际金奖
涂料行业唯一!三棵树AI公益项目获艾菲国际金奖
 三棵树 X 抖音《心动的房子》,明星携手顶尖设计师,开启“理想家”的美学探索
三棵树 X 抖音《心动的房子》,明星携手顶尖设计师,开启“理想家”的美学探索
 三棵树越南市场开拓:深耕本土化运营 打造东南亚发展新样本
三棵树越南市场开拓:深耕本土化运营 打造东南亚发展新样本
 工程机械销量上扬引涂料需求爆发,高性能+环保+国产化重塑行业格局
工程机械销量上扬引涂料需求爆发,高性能+环保+国产化重塑行业格局
 政策破局+需求牵引:中国特种涂料产业正迎来"自主突围"黄金窗口期!
政策破局+需求牵引:中国特种涂料产业正迎来"自主突围"黄金窗口期!
 中国涂层材料行业全景透视:市场规模同比增长2.62%背后的工业驱动与创新趋势!
中国涂层材料行业全景透视:市场规模同比增长2.62%背后的工业驱动与创新趋势!
 纳米涂层赋能新能源产业破局!
纳米涂层赋能新能源产业破局!
 80亿市场规模背后的绿色革命:无机涂料何以成为建材行业新宠?
80亿市场规模背后的绿色革命:无机涂料何以成为建材行业新宠?
 防水行业从“增量红利”到“存量博弈”!
防水行业从“增量红利”到“存量博弈”!
 辐射制冷涂料以“智冷”技术开启涂料产业新增长极!
辐射制冷涂料以“智冷”技术开启涂料产业新增长极!
 基建“三稳”赋能,为涂料行业带来哪些机会?
基建“三稳”赋能,为涂料行业带来哪些机会?
 三棵树即将亮相2025广州设计周:以东方美学开启温情之旅
三棵树即将亮相2025广州设计周:以东方美学开启温情之旅
 【月满东方 宅见未来】三棵树以“东方大宅”为笺,亮相2025广州设计周
【月满东方 宅见未来】三棵树以“东方大宅”为笺,亮相2025广州设计周
 钛白粉:出口回暖,增长能否延续?
钛白粉:出口回暖,增长能否延续?
